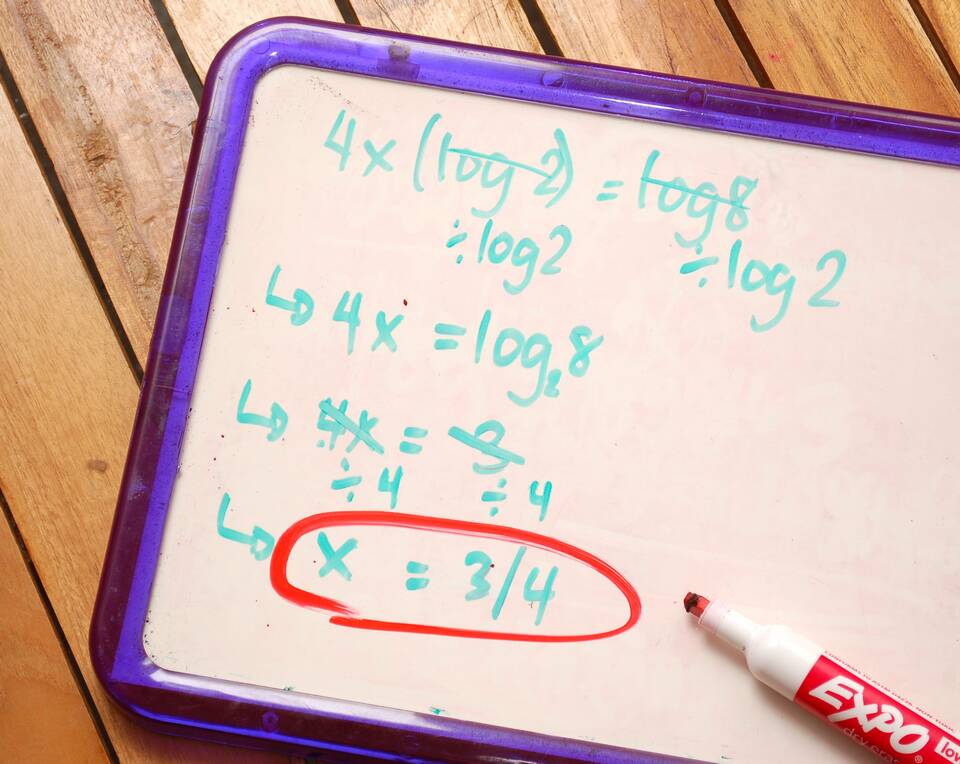Сумма логарифмов с одинаковым основанием подчиняется фундаментальному логарифмическому тождеству. Для любых положительных чисел a, b и основания c (c > 0, c ≠ 1) выполняется равенство:
Содержание
Основное свойство суммы логарифмов
| logca + logcb | = | logc(a × b) |
Доказательство свойства
- Пусть logca = x ⇒ cx = a
- Пусть logcb = y ⇒ cy = b
- Перемножим равенства: cx × cy = a × b
- По свойству степеней: cx+y = a × b
- По определению логарифма: x + y = logc(a × b)
- Следовательно: logca + logcb = logc(a × b)
Обобщение для n слагаемых
Свойство можно расширить на произвольное количество слагаемых:
- logca1 + logca2 + ... + logcan
- = logc(a1 × a2 × ... × an)
Примеры применения
| Пример | Решение |
| log28 + log24 | = log2(8×4) = log232 = 5 |
| log10100 + log101000 | = log10(100×1000) = log10100000 = 5 |
| ln e + ln e2 | = ln(e × e2) = ln e3 = 3 |
Ограничения и особенности
- Основание логарифма должно быть одинаковым
- Все аргументы логарифмов должны быть положительными
- Основание не может быть равно 1
- Свойство не работает для разности логарифмов
Практическое применение
Данное свойство широко используется в:
- Упрощении сложных логарифмических выражений
- Решении логарифмических уравнений
- Вычислениях в математическом анализе
- Теории вероятностей и статистике
- Компьютерных науках и теории информации
Заключение
Свойство суммы логарифмов с одинаковым основанием является важным инструментом в математике, позволяющим преобразовывать и упрощать сложные выражения. Понимание этого свойства необходимо для решения широкого круга задач в различных областях науки и техники.